在《星露谷物语》中,玛鲁的物理题目可能让你困惑,尤其是关于气体分压的计算。本文详细解答了一个示例问题:在0.80个标准大气压下,如何计算一氧化碳的分压。跟随攻略的步骤,你将学会如何应用道尔顿分压定律,并得出正确答案0.24个标准大气压。如果你在游戏中遇到类似的物理难题,不妨参考这篇攻略,它会帮助你轻松过关。
星露谷物语玛鲁物理题答案是什么
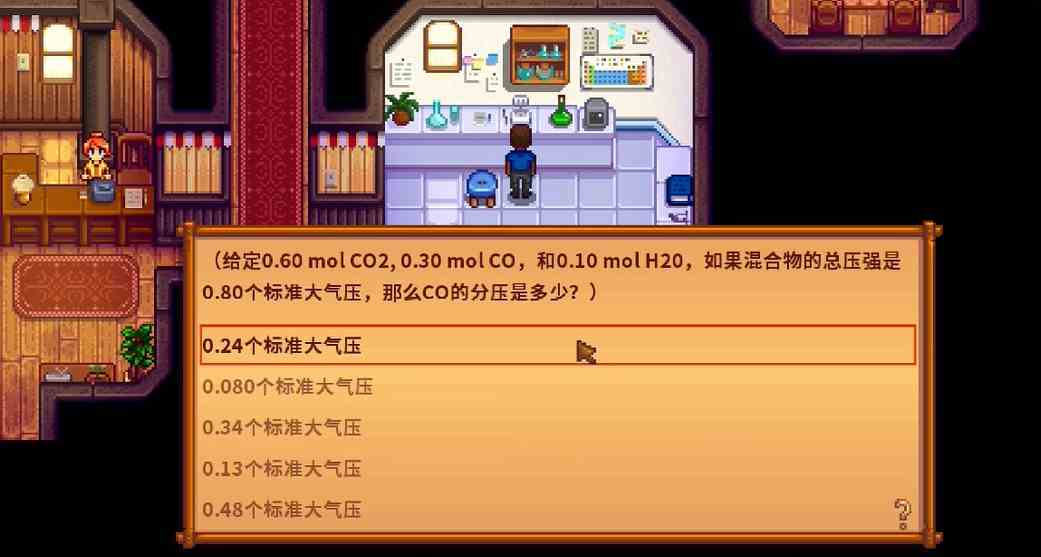
问:给定0.60molC02,0.30molC0,和0.10molH20,如果混合物的总压强是0.80个标准大气压,那么C0的分压是多少?
答:0.24个标准大气压
1、0.24个标准大气压
2、0.080个标准大气压
3、0.34个标准大气压
4、0.13个标准大气压
5、0.48个标准大气压

答案解析:
1、圆的周长 \( C \) 与其半径 \( r \) 之间的关联可表示为:\[lbk] C = 2\pi r \[rbk]根据给定条件,圆周正以每分钟0.5米的速率扩展,即:\[lbk] \frac{dC}{dt} = 0.5 \text{ m/min} \[rbk]目前,我们旨在确定半径 \( r = 4 \) 米时,圆的面积变化率。
2、面积的公式为 \( A = \pi r^2 \)。首先,我们需推导出面积变化率 \(\frac{dA}{dt}\),通过链式法则,可得:\[lbk] \frac{dA}{dt} = \frac{dA}{dr} \cdot \frac{dr}{dt} \[rbk]由 \( A = \pi r^2 \),对 \( r \) 求导得:\[lbk] \frac{dA}{dr} = 2\pi r \[rbk]接下来,需计算 \(\frac{dr}{dt}\)。
3、由 \( C = 2\pi r \),对 \( t \) 求导得:\[lbk] \frac{dC}{dt} = 2\pi \frac{dr}{dt} \[rbk]将 \(\frac{dC}{dt} = 0.5 \) 代入上式,得:\[lbk] 0.5 = 2\pi \frac{dr}{dt} \[rbk]解得 \(\frac{dr}{dt} = \frac{0.5}{2\pi} = \frac{1}{4\pi} \text{ m/min}\)。故:\[lbk] \frac{dA}{dt} = 2\pi r \cdot \frac{1}{4\pi} = \frac{r}{2} \[rbk]当 \( r = 4 \) 米时,\[lbk] \frac{dA}{dt} = \frac{4}{2} = 2 \text{ m}^2/\text{min} \[rbk]因此,半径为4米时,圆的面积每分钟增长2平方米。
4、对于一氧化碳在总压0.8大气压的混合物中的分压计算,我们借助道尔顿分压定律。该定律表明,混合气体的总压强等于各组分气体分压强的总和。
5、一氧化碳的分压可由其摩尔比乘以总压强获得。已知条件为:- 在1大气压下,二氧化碳、一氧化碳和水的摩尔数分别为0.6、0.3和0.1。- 总摩尔数 \( n_{total} = 0.6 + 0.3 + 0.1 = 1 \) 摩尔。计算摩尔比得:- 二氧化碳的摩尔比 \( x_{CO2} = \frac{0.6}{1} = 0.6 \)- 一氧化碳的摩尔比 \( x_{CO} = \frac{0.3}{1} = 0.3 \)- 水蒸气的摩尔比 \( x_{H2O} = \frac{0.1}{1} = 0.1 \)若总压强降为0.8大气压,则一氧化碳的分压 \( P_{CO} \) 可通过\[lbk] P_{CO} = x_{CO} \times P_{total} \[rbk]计算,其中 \( x_{CO} = 0.3 \) 且 \( P_{total} = 0.8 \) 大气压。
6、因此:\[lbk] P_{CO} = 0.3 \times 0.8 = 0.24 \text{大气压} \[rbk]所以,当混合物总压为0.8大气压时,一氧化碳的分压为0.24大气压。